说明

早些日子，我写过一篇《面向对象的反思》，这文章中我极大的提出OOP的一些问题。同时也设想般的认为用FP的方式去解决这些问题会非常容易。直到读到这篇文章《Clash of Styles, Part #3 – Extensibility via OOP and FP》，这篇文章对比了OOP和FP的扩展性，并对这两种扩展性作出了对比和说明。看完觉得自己还是太天真了，OOP和FP在不同的需求下会表现出不同的扩展能力，是一篇好文章，逐翻译如下。

介绍

在这个系列的Part 1和Part 2中，我比较了两种本质是上正交的编程风格：面向对象的编程风格(OOP)和函数式风格(FP)。你会看到使用相反的方式来实现同样功能的示例。

你会看到需求被放到一个二维表格中，称为Operations Matrix。行表示不同的变量(类型)，列表示这些变量(类型)支持的操作。

如果软件在写完后是一成不变的，故事到这里就结束了。任何人不用多久就能知道这个假设多天真，需求是不可预测，不停在变。

这也是编程中最有意思的部分：怎么样让未来修改和扩展更容易，而不是将已有的部分扔掉重来？什么是容易扩展？在FP和OOP中什么样的扩展是容易实现的。

这篇文章就是回答这些问题，接着读吧！

从Operations Matrix角度看扩展

回忆一下我们的前面简单解释器的Operations Matrix，看起来是这个样子的：

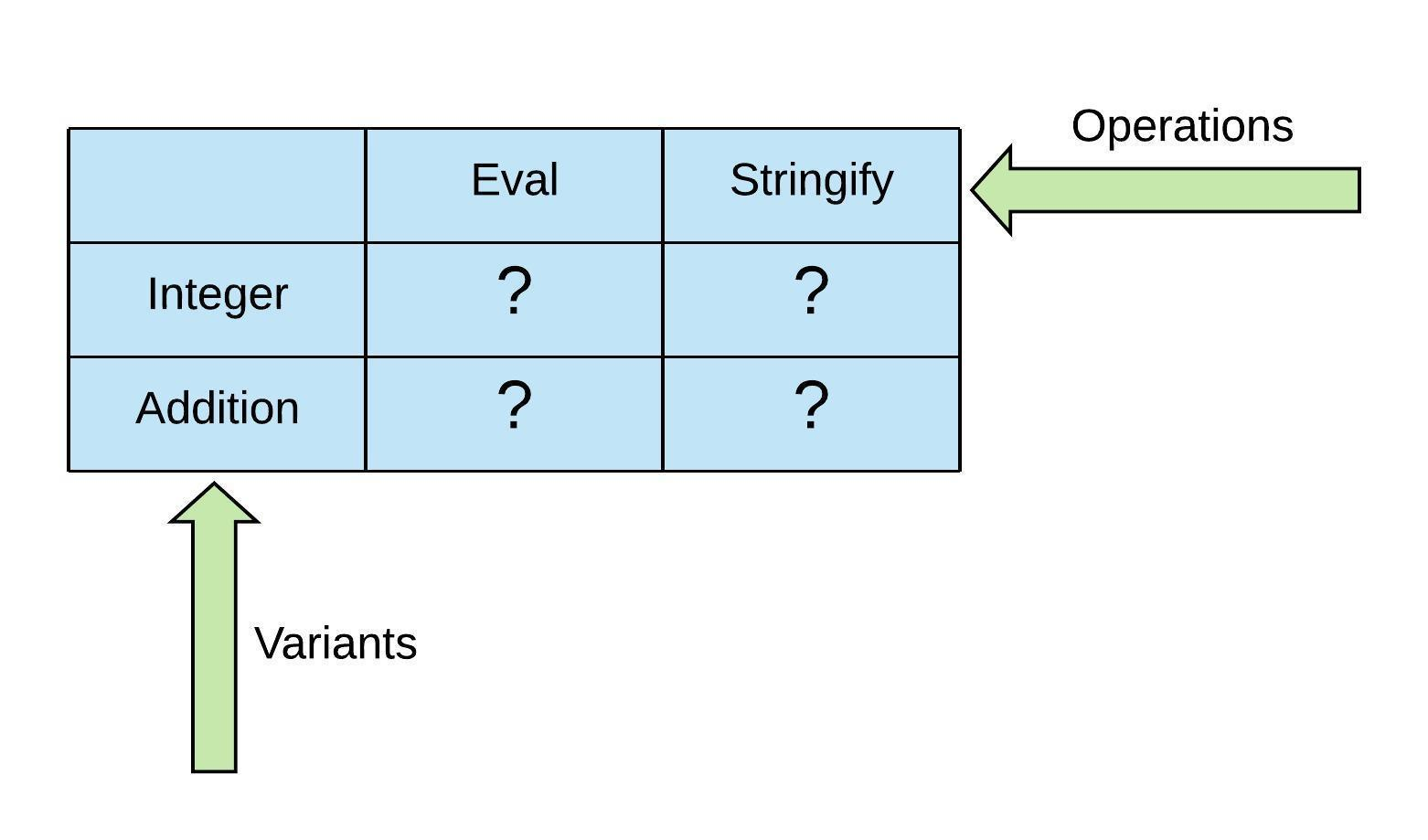
目前为止，我们已经支持对变量Integer Constant和Addition的两种操作：Eval和Stringify。在这个系列的前两部分，我们用填格子的方式实现了我们的需求，就是图中这些问号。我们开始使用OOP的方式来实现，接着用FP的方式实现一次。

本文主要是关于怎么样扩展Operations Matrix。也就覆盖我们新增需求的格子。格子会发生两个方向上的变化：添加新的类型--增加行。或是添加新的操作--增加列。

OOP和FP风格不同，针对两个不同的需求(增加类型还是操作符），实现上难度也不同。

下表描述了从OOP和FP的角度来看，扩展现有程序来实现需求的难易程度：

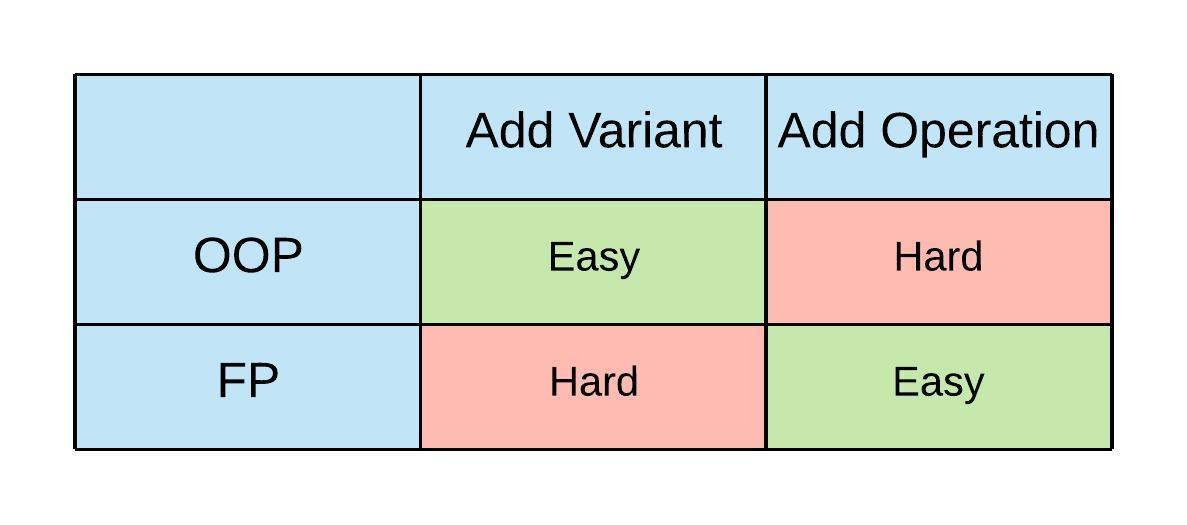
对OOP来讲，添加类型很容易，但是增加操作却比较难。而FP却正好相反。为什么会这样？放到SOLID中Open-Closed原则的上下文中比较容易解释清楚。

OOP和FP的开放封闭原则

程序应该对扩展开放（容易扩展），对修改封闭（不需要改变已有的部分）。

这什么意思呢？

归根到底就是以什么样的方式设计我们的程序，让未来实现新的需求或改变时候，尽量不需要修改已有的代码。为什么要这样？因为修改代码太难了，太容易犯错了。当前完善的测试可以大大减少这种风险，但仍有很大机会会搞砸。

关于SOLID原则的文章有很多。如果你想更深入的了解SOLID原则，我建议阅读SOLID原则创建者Robert C. Martin的《敏捷软件开发 : 原则、模式与实践》。然而这本书和其他类似的文章都是从主要从OOP的角度来看，这不完善，我这里从FP的角度来看，让整个原则更加完整。

这里我想集中讨论一下OCP(Open-Closed Principle)在FP和OOP中的对比。

怎么样增加新功能却不用修改已有代码？这是不是听起来很矛盾？如果我们要修改程序，我们肯定要修改代码。

矛盾也不矛盾。我们设想程序被设计成一个工具箱。我们工具箱中有大量的工具供我们使用。当我们需要新工具的时候，我们就去找来新工具，然后使用新的工具来完成任务。这些工具都很容易使用，它可以很好完成自己的本职工作——不是自己的本职工作，它也做不了。（译注：怎不能用扳手钻洞吧。）

如果找不到这样的工具怎么办，我们就做一个。这就是我们扩展工具箱的方式。我们不会魔改我们现有的工具去让这个工具去干不是它本职工作的事。这样工具就没有通用性了。

在OOP中，这些工具就是对象。我们可以通过添加新的类型和对象来实现不修改现有代码来扩展程序。

在FP中，这些工具就是函数。可以通过添加新的函数来扩展程序，并且不用修改已有的代码。

但，如果反过来给OOP中的对象们添加新的函数，或者FP中给函数们添加新的类型支持。这样的情况会让这两种编程范式头疼，逼着我们修改已有的类型或者函数。

严格上讲，通过前期的精妙设计，可以让OOP和FP支持这些对他们来说有些“不自然”的扩展。我们会在本文最后讨论，也会有篇文章来探讨这些细节。

当下，让我们务实点，看看OOP和FP分别怎么样添加类型和函数。

添加类型

在我们的解释器中添加一个类型，支持一个新的表达式。这里我用取反Negation表达式。新的类型在Operations Matrix中用行来表示。

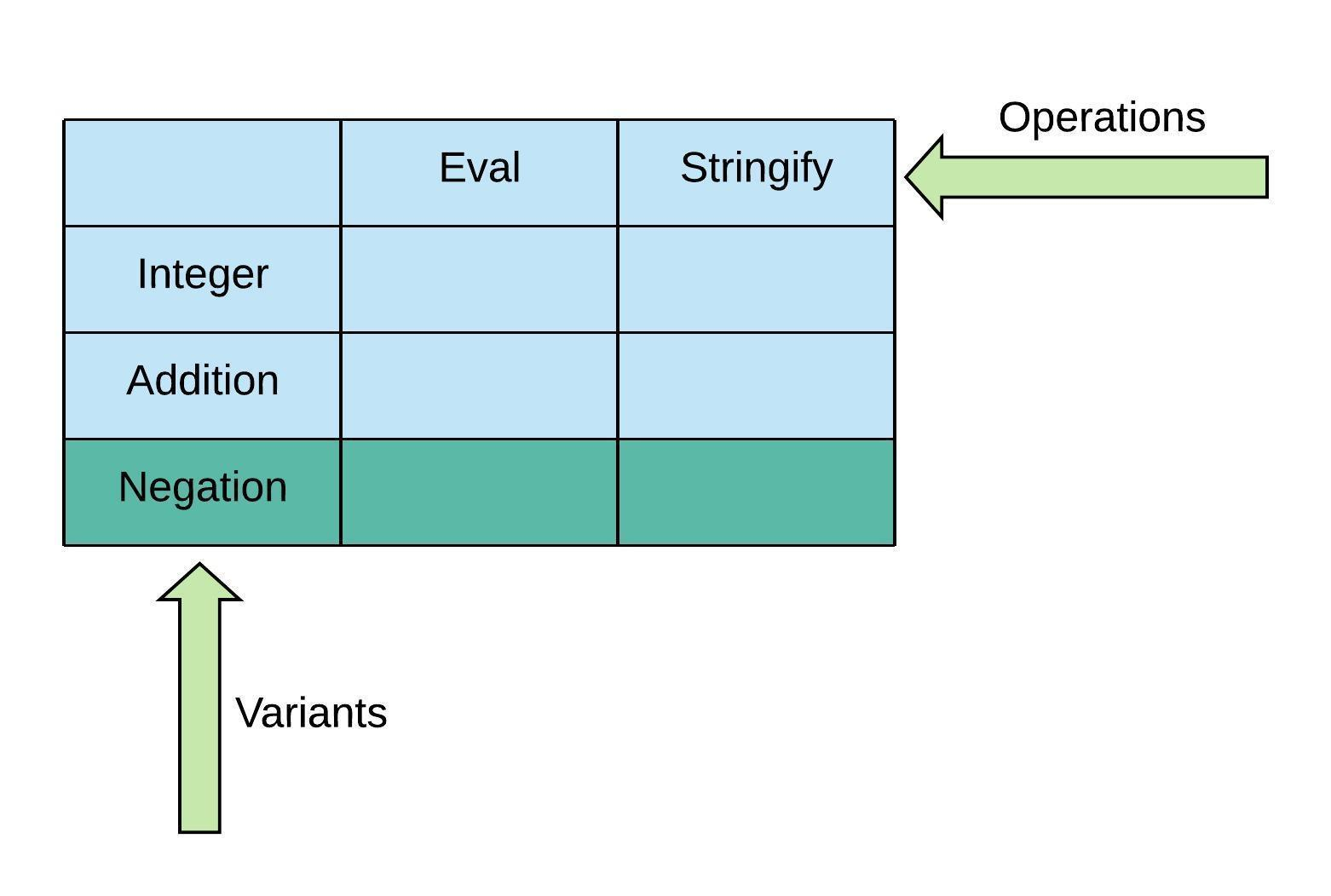
让我先用OOP来实现这个扩展——支持新的类型。

给OOP添加类型

前面说过，OOP在行上扩展Operations Maxtrix。每个表达式类型自己去实现相应的函数。Negation类型也不例外：

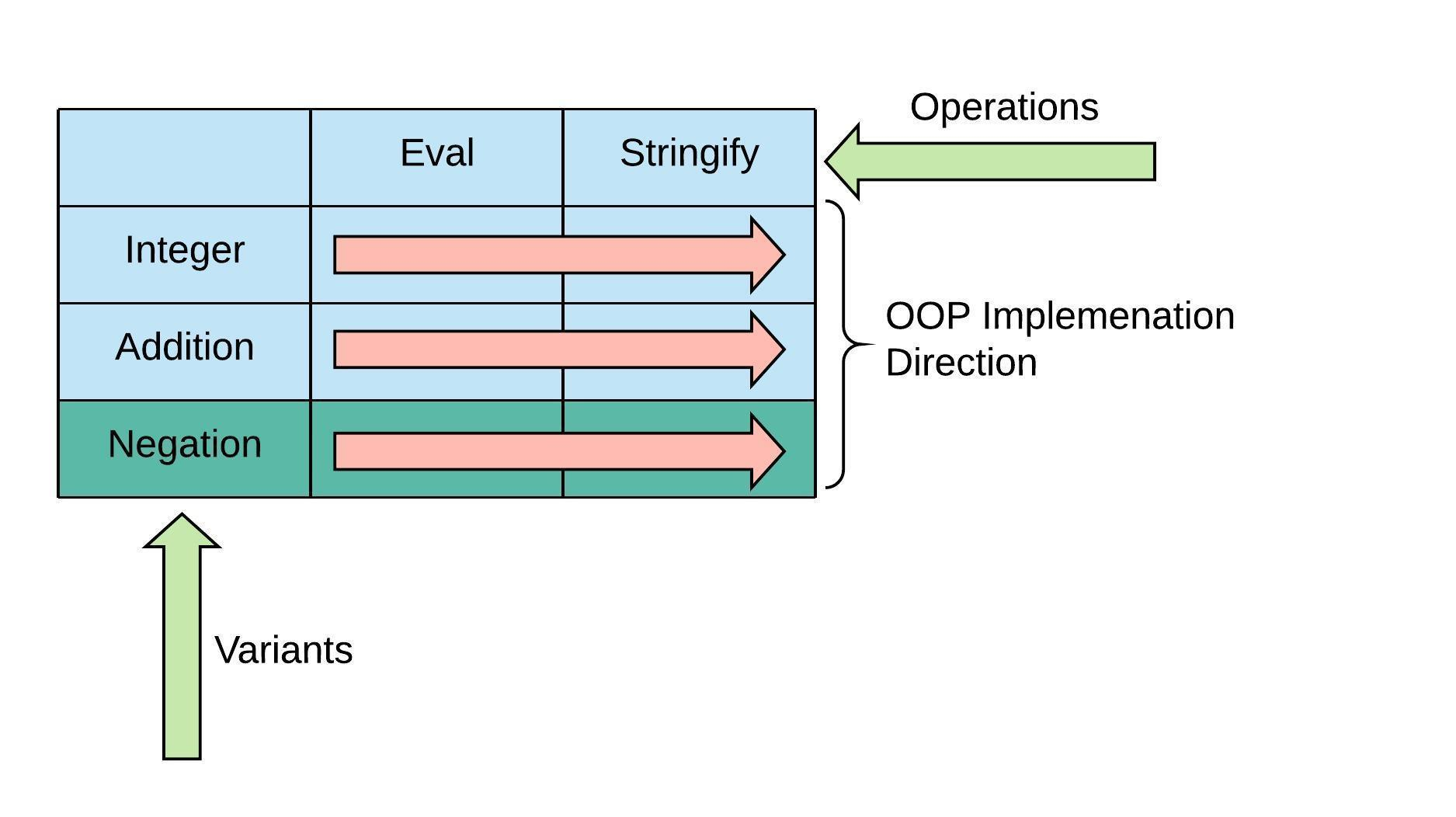
从代码角度来看，就是新增一个Negation类型，这个Negation类型实现了Eval和Stringify函数：

public class Negation : IExpression
{
    private readonly IExpression _expression;

    public Negation(IExpression expression)
    {
        _expression = expression;
    }

    public int Eval()
    {
        return -_expression.Eval();
    }

    public string Stringify()
    {
        return $"-({_expression.Stringify()})";
    }
}

重要的不是怎么样实现，而且我们仅通过添加一个新的类型就扩展了我们的程序。这是一个"容易"的扩展。我们没有改动任何老代码，所以也不会有任何回归风险，是符合OCP原则的。

让我们反过来看看FP是怎么样实现新添加的类型的。

在FP中添加新类型

在Operations Matrix中，FP的实现是纵向的。FP中关键元素是函数。每个函数实现一个操作。在这样情况下，添加新的类型意味着已有的函数必须做一些改动。

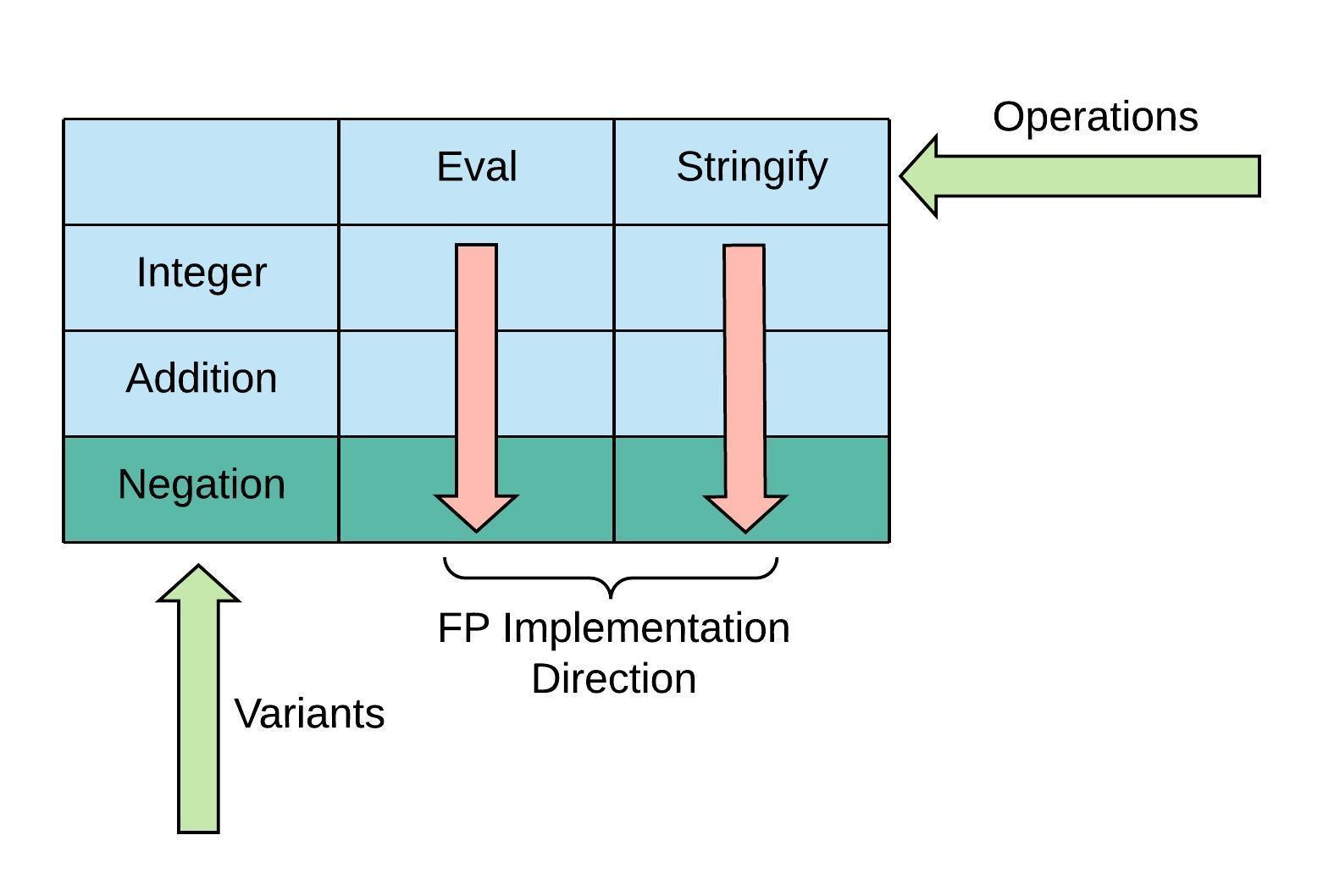
所有现有的操作函数都必须执行这个新加的行(类型)。这让我们必须修改现有函数。首先，我们需要扩展我们的Expression类型，让他支持新加的Negation类型

type Expression =
    | MyInt of int
    | Addition of Expression * Expression
    | Negation of Expression

接着我们修改eval函数，添加一个新的处理。

let rec eval expression =
    match expression with
    | MyInt i -> i
    | Addition (op1, op2) -> eval op1 + eval op2
    | Negation exp -> -eval exp

stringify也是同样的：

let rec stringify expression =
    match expression with
    | MyInt i -> i.ToString()
    | Addition (op1, op2) -> stringify op1 + " + " + stringify op2
    | Negation exp -> "-(" + stringify exp + ")"

这就是“困难”修改的例子。我们必须修改每个使用Expression的函数，这很明显的违反了OCP原则。

这里示例过于简单，所以改起来还不难。想想现实中的例子，通过修改已有的代码来添加新功能是很容易出错的。

让我们看看光谱的另一端，看如何在给我们的解释器添加一个操作函数。

添加操作

新的操作函数叫做CountZeros，相当简单，就是看看表达式中有多少个0。

在Operations Matrix中意味着添加一列：

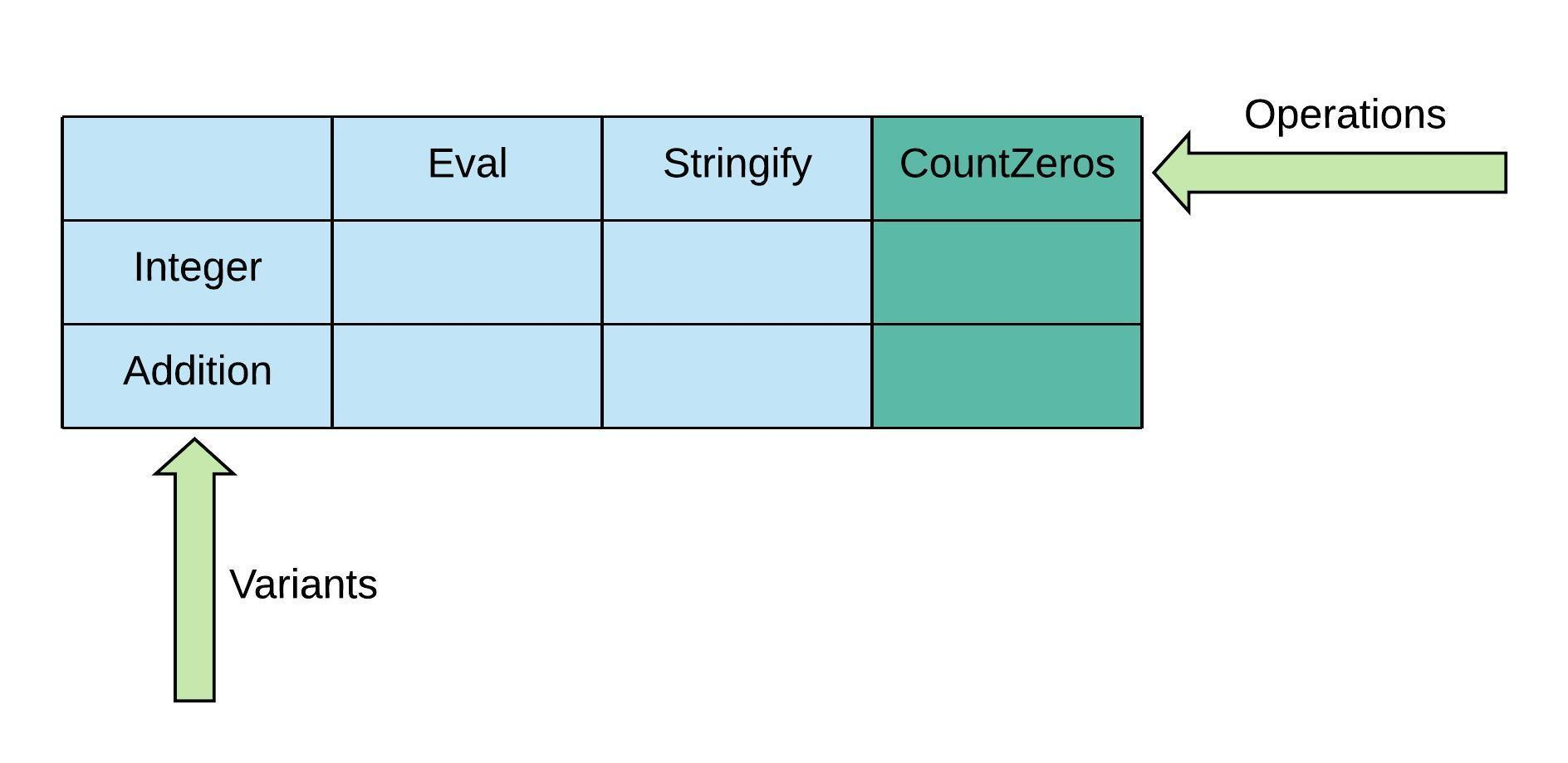
如果你的直觉告诉你这在函数式风格中很容易实现，那么，你对了。

让我们看看实现细节。

在FP中添加操作

FP以列的方式实现Operations Matrix中的功能。每种操作都会考虑他所支持的所有表达式(Expression)。非常适用于CountZeroes的实现。

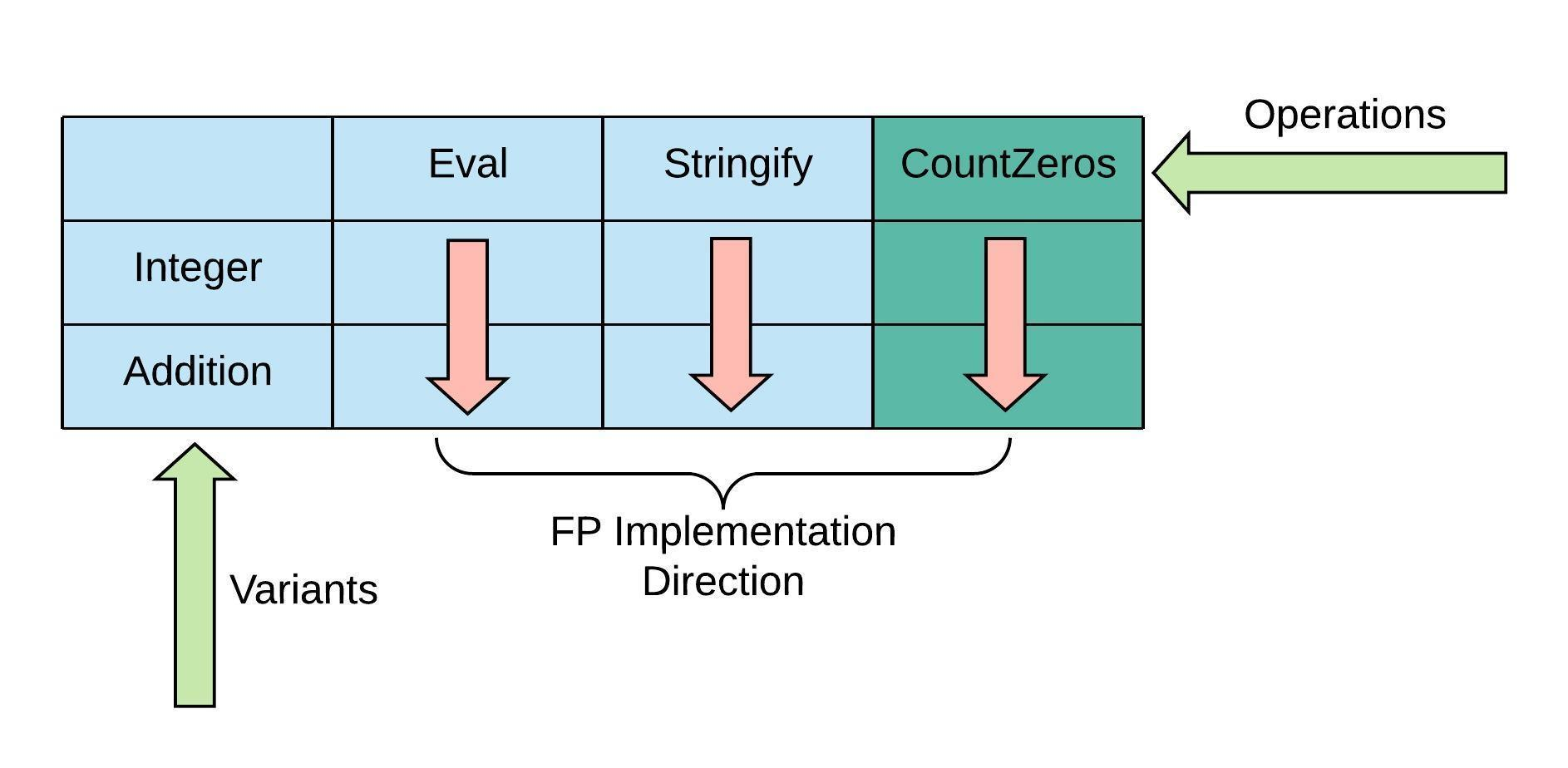
在FP中添加一个操作就是实现一个新的函数：

let rec countZeros expression =
    match expression with
    | MyInt i -> if i = 0 then 1 else 0
    | Addition (op1, op2) -> countZeros op1 + countZeros op2

这也是为什么在FP中添加操作非常“容易”的原因。

同时由于这两种范式是正交的，我们不难想象OOP在实现这样的扩展的时候会有困难，让我们看一下，确认一下。

在OOP中添加操作

在OOP中，添加操作跟在FP中添加类型一样会非常困难。本例中CountZeroes横跨所有的类型，这也意味着所有类型必须修改以支持新的操作。

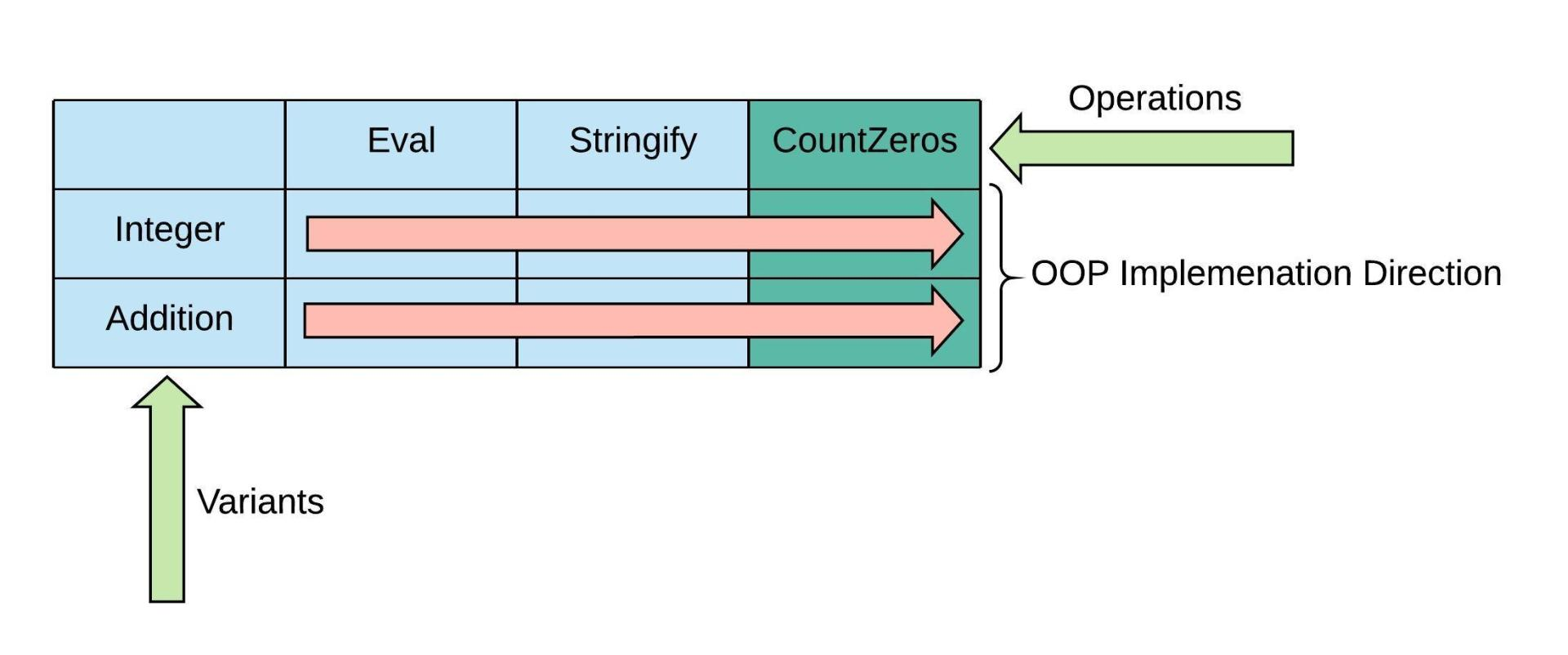
从代码上来看，我们首先要扩展IExpression接口。

public interface IExpression
{
    int Eval();

    string Stringify();

    int CountZeros();
}

接着给MyInt新增一个函数：

public class MyInt : IExpression
{
    private int Val { get; } 

    public MyInt(int val)
    {
        Val = val;
    }

    public int Eval() => Val;
    public string Stringify() => Val.ToString();
    public int CountZeros() => Val == 0 ? 1 : 0;
}

接着修改Addition类：

public class Addition : IExpression
{
    private readonly IExpression _operand1;
    private readonly IExpression _operand2;

    public Addition(IExpression operand1, IExpression operand2)
    {
        _operand1 = operand1;
        _operand2 = operand2;
    }

    public int Eval() => _operand1.Eval() + _operand2.Eval();
    public string Stringify() => $"{_operand1.Stringify()} + {_operand2.Stringify()}";
    public int CountZeros() => _operand1.CountZeros() + _operand2.CountZeros();
}

这跟我们在FP中添加类型一模一样，需要修改好几处代码。

中间地带

基于目前的讨论，你可能对程序未来的扩展方向很有信心，这样你就能选择相应的编程风格。如果选对了，你就舒服了。如果你选错了，你就倒霉了。每当你要扩展你的程序的时候，你就要进行一些“危险的”代码修改。

幸运的是，现实不可能是这样的。首先，你就不可能100%的预测程序的扩展方向。其次，很少有情况你只需要扩展一种，大部分情况，你既要扩展类型，也要添加新的操作支持。

还好，我们可以预先做一些工作。让这些对FP和OOP来说困难的扩展方式变得容易一点。在OOP中，我们甚至发明了一个词：Visitor模式。我会在未来的文章中详细介绍。

尽管，可以给FP或者OOP添加一些“不自然”的扩展。但是也让你的程序代码或多或少的看上去有点奇怪。这也是为什么对程序未来有什么样的修改需要做一个预判。

不管你怎么做，总有一些情况让你最初的选择出现了偏差。你需要接受这个事实，同时积极修复这个错误。

未来难以预测

事实上，你对未来的修改做计划本身就是一件非常困难的事。你可能不知道未来程序会以什么样的方式扩展，或者你能预料到会在两个方向上都要扩展。无论哪样，都挺难办。

扩展性是把双刃剑。他确实让代码更通用，更易重用。但是也让程序变的难懂。

同样过多的提前设计分析也会进入一种“分析瘫痪”状态。我坚信设计是从现有实现中浮现出来的。我们越是修改，越是知道哪里容易修改，我们越是知道什么样的模型/抽象是正确的。一开始，我们啥也不懂，很难直接做好。

这也就是说，当遇到一个新问题的时候，不要过分的提前设计，追求完美。这基本不可能的。从简单的尝试开始，画画示例图，写写示例代码。一遍又一遍地重复这个过程。不要怕进行大的修改(没有稳定的单元测试会难上加难)。根据这里的建议，我确定你会最终会有一个优雅的，可维护的，客户喜欢使用的系统。

总结

在本篇文章中，你看到了在OOP和FP中选择一种，并不是风格差异或个人喜好这么简单。这也影响着程序未来的可维护性。

我们看到了OOP以一种自然的方式让添加新的类型比较容易，同时在FP中添加新的操作更加容易。

这个系列接下来的部分，你会更深入地了解一些更加具体特例，看看FP和OOP怎么样处理这些特例。这也让我们引出了更加高级的技术，像Double Dispatch。

我会介绍一些设计模式，借此来让OOP和FP中更好地支持这些“不自然”扩展。

感谢你的阅读！继续关注这个系列接下来的文章。

后记

把Robert C. Martin的书拿出来重新翻了翻，这书是2010年1月1日买的。我也看了，但是你能说我当时看了就理解了么？我当时是理解了，但是我并不会用。十年学会编程一点都不假。